Data Structures Cheat Sheet

To see a video of where I explain how these data structures work, please watch this youtube video.

The C++ Data Structure Cheat Sheet!

I, like many other software developers, switch programming languages depending on project needs or if I'm learning something new. When coming back to a language that you haven't used in a while, often a refresher is needed to make sure syntax is correct. This is especially true for the correct usage of data structures.
C++ happens to be my preferred programming language for algorithm contests, and so I've created this page to hold example code for each important data structure for C++. It'll be a great reference for anyone that uses the language to see all of the data structures in action.
Without further ado, let's get into example code for each data structure. You can download this code yourself on github, found here.)

Arrays

Output:
C++ Array Code
Unsorted array:
Index 0 holds the number 10.
Index 1 holds the number 9.
Index 2 holds the number 8.
Index 3 holds the number 7.
Index 4 holds the number 6.
Index 5 holds the number 5.
Index 6 holds the number 4.
Index 7 holds the number 3.
Index 8 holds the number 2.
Index 9 holds the number 1.
Sorted array:
Index 0 holds the number 1.
Index 1 holds the number 2.
Index 2 holds the number 3.
Index 3 holds the number 4.
Index 4 holds the number 5.
Index 5 holds the number 6.
Index 6 holds the number 7.
Index 7 holds the number 8.
Index 8 holds the number 9.
Index 9 holds the number 10.

Vectors

Output:
C++ Vector Code,
Unsorted vector:
4 3 2 1
Sorted vector:
1 2 3 4
Vector of vectors:
1 2 3
4 5 6
7 8 9

Stacks

Output:
C++ Stack Code
Printed stack:
3 1 2 4
Printed Food stack:
Food number 1 has 4 of French Fries and it tastes good!
Food number 2 has 3 of Chocolate and it tastes good!
Food number 3 has 5 of Eclair and it tastes good!
Food number 4 has 2 of Banana and it tastes good!
Food number 5 has 1 of Apple and it tastes bad!

Queues

Output:
C++ Queue Code
Printed queue:
4 2 1 3
Printed Food queue:
Food number 1 has 1 of Apple and it tastes bad!
Food number 2 has 2 of Banana and it tastes good!
Food number 3 has 5 of Eclair and it tastes good!
Food number 4 has 3 of Chocolate and it tastes good!
Food number 5 has 4 of French Fries and it tastes good!

Priority Queues

Output:
C++ Priority Queue Code
Printed priority queue:
6 5 4 3 2 2 1
Printed Food priority queue:
Food number 1 has 1 of Apple and it tastes bad!
Food number 2 has 2 of Banana and it tastes good!
Food number 3 has 3 of Chocolate and it tastes good!
Food number 4 has 4 of French Fries and it tastes good!
Food number 5 has 5 of Eclair and it tastes good!

Sets

Output:
C++ Set Code
Printing the numbers in the set:
1 2 3 4
2 is no longer in the set.
Printing the Food in the food set:
Food number 1 has 1 of Apple and it tastes bad!
Food number 2 has 2 of Banana and it tastes good!
Food number 3 has 3 of Banana and it tastes good!
Food number 4 has 4 of Donut and it tastes good!

Unordered Sets

I'm pretty sure that the operations are exactly the same as set; only the initialization name and library name are different. (Anywhere the word 'set' is, replace with 'unordered_set'.)
The difference is the underlying data structure used. Sets use red-black BSTs, which means it's in order, but unordered_sets use hash maps as their underlying data structure, which means order isn't preserved.

Unordered Maps

Output:
C++ Unordered Map Code
Printing map using iterators:
Donut: 295
Chocolate: 1000
Banana: 100
Apple: 1
Did not find Taylor Swift in our map.
0
We have 100 Nachos and it tastes good.
We have 3 Mango and it tastes good.
We have 20 Lemons and it tastes bad.

Lists (Linked Lists)

We've made a Linked List tutorial for anyone new to the data structure itself, but the code we'll write here is for the List data structure from C++'s standard library. It's the same as a regular linked list, but with STL features.

Output:
Program began.
srcmake is really very awesome.
Program ended.

Please watch the following video to see me explain how these data structures work:

Like this content and want more? Feel free to look around and find another blog post that interests you. You can also contact me through one of the various social media channels.
Twitter: @srcmake
Discord: srcmake#3644
Youtube: srcmake
Twitch: www.twitch.tv/srcmake
Github: srcmake

Comments are closed.

Common Data Structure Operations

Java Algorithms And Data Structures Cheat Sheet

R Data Structures Cheat Sheet

DATA STRUCTURES CHEAT SHEET Python - Data Structure It is a way of organizing data that contains the items stored and their relationship to each other The areas in which Data Structures are applied:. Compiler design. Operating system. Database Management System. Statistical Analysis Package. Numerical Analysis. Graphics. Adobe master collection cs4 serial number. Nov 29, 2017 - Explore Angel Ortega's board 'Data Structures and Algorithms Cheat Sheets' on Pinterest. See more ideas about data structures, algorithm, cheat sheets.

This part mainly focuses on common snippets in Python code. The cheat sheet not only includes basic Python features but also data structures and algorithms.
About: I made this website as a fun project to help me understand better: algorithms, data structures and big O notation. And also to have some practice in: Java.

Python Algorithm Cheat Sheet

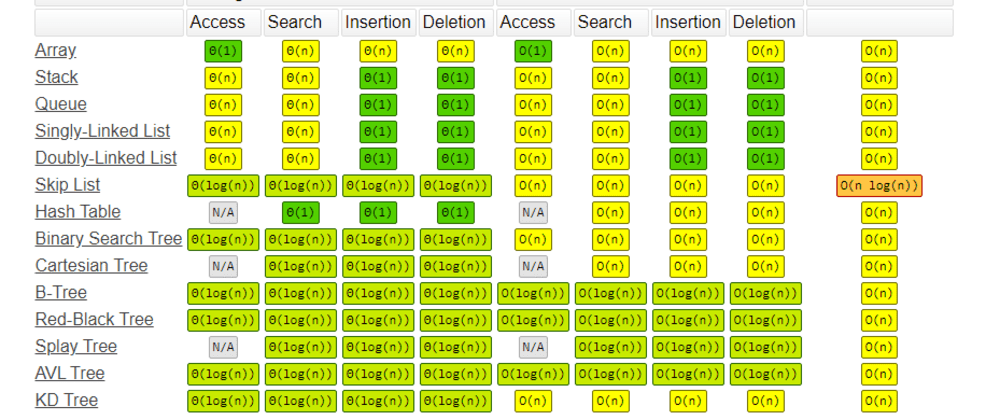
Data Structure	Time Complexity								Space Complexity
Average				Worst				Worst
Access	Search	Insertion	Deletion	Access	Search	Insertion	Deletion
Array	`Θ(1)`	`Θ(n)`	`Θ(n)`	`Θ(n)`	`O(1)`	`O(n)`	`O(n)`	`O(n)`	`O(n)`
Stack	`Θ(n)`	`Θ(n)`	`Θ(1)`	`Θ(1)`	`O(n)`	`O(n)`	`O(1)`	`O(1)`	`O(n)`
Queue	`Θ(n)`	`Θ(n)`	`Θ(1)`	`Θ(1)`	`O(n)`	`O(n)`	`O(1)`	`O(1)`	`O(n)`
Singly-Linked List	`Θ(n)`	`Θ(n)`	`Θ(1)`	`Θ(1)`	`O(n)`	`O(n)`	`O(1)`	`O(1)`	`O(n)`
Doubly-Linked List	`Θ(n)`	`Θ(n)`	`Θ(1)`	`Θ(1)`	`O(n)`	`O(n)`	`O(1)`	`O(1)`	`O(n)`
Skip List	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`O(n)`	`O(n)`	`O(n)`	`O(n)`	`O(n log(n))`
Hash Table	`N/A`	`Θ(1)`	`Θ(1)`	`Θ(1)`	`N/A`	`O(n)`	`O(n)`	`O(n)`	`O(n)`
Binary Search Tree	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`O(n)`	`O(n)`	`O(n)`	`O(n)`	`O(n)`
Cartesian Tree	`N/A`	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`N/A`	`O(n)`	`O(n)`	`O(n)`	`O(n)`
B-Tree	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`O(log(n))`	`O(log(n))`	`O(log(n))`	`O(log(n))`	`O(n)`
Red-Black Tree	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`O(log(n))`	`O(log(n))`	`O(log(n))`	`O(log(n))`	`O(n)`
Splay Tree	`N/A`	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`N/A`	`O(log(n))`	`O(log(n))`	`O(log(n))`	`O(n)`
AVL Tree	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`O(log(n))`	`O(log(n))`	`O(log(n))`	`O(log(n))`	`O(n)`
KD Tree	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`Θ(log(n))`	`O(n)`	`O(n)`	`O(n)`	`O(n)`	`O(n)`

Data Structures Cheat Sheet Pdf

Array Sorting Algorithms

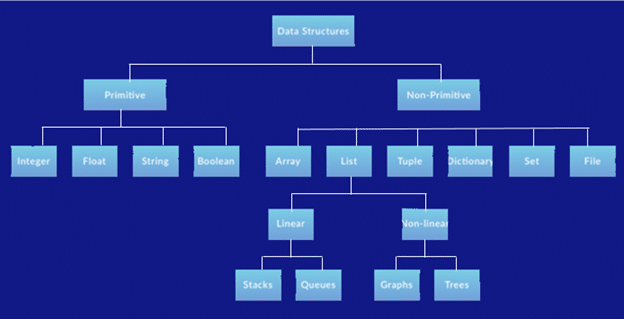
Algorithm	Time Complexity			Space Complexity
Best	Average	Worst	Worst
Quicksort	`Ω(n log(n))`	`Θ(n log(n))`	`O(n^2)`	`O(log(n))`
Mergesort	`Ω(n log(n))`	`Θ(n log(n))`	`O(n log(n))`	`O(n)`
Timsort	`Ω(n)`	`Θ(n log(n))`	`O(n log(n))`	`O(n)`
Heapsort	`Ω(n log(n))`	`Θ(n log(n))`	`O(n log(n))`	`O(1)`
Bubble Sort	`Ω(n)`	`Θ(n^2)`	`O(n^2)`	`O(1)`
Insertion Sort	`Ω(n)`	`Θ(n^2)`	`O(n^2)`	`O(1)`
Selection Sort	`Ω(n^2)`	`Θ(n^2)`	`O(n^2)`	`O(1)`
Tree Sort	`Ω(n log(n))`	`Θ(n log(n))`	`O(n^2)`	`O(n)`
Shell Sort	`Ω(n log(n))`	`Θ(n(log(n))^2)`	`O(n(log(n))^2)`	`O(1)`
Bucket Sort	`Ω(n+k)`	`Θ(n+k)`	`O(n^2)`	`O(n)`
Radix Sort	`Ω(nk)`	`Θ(nk)`	`O(nk)`	`O(n+k)`
Counting Sort	`Ω(n+k)`	`Θ(n+k)`	`O(n+k)`	`O(k)`
Cubesort	`Ω(n)`	`Θ(n log(n))`	`O(n log(n))`	`O(n)`